Fuzzy logic introduction
Fuzzy logic is a type of logic that allows for degrees of truth rather than just binary true/false values. It is a mathematical framework that can be used to model complex systems and make decisions based on incomplete or uncertain information. In this blog post, we will explore the basics of fuzzy logic and how it works.
What is Fuzzy Logic?
Fuzzy logic was first introduced in the 1960s by Lotfi Zadeh, a professor at the University of California, Berkeley. It is a type of logic that is based on the concept of fuzzy sets, which are sets that have degrees of membership rather than strict membership. This means that elements can belong to a set to varying degrees, rather than just being either in or out of the set.
Fuzzy logic is used to deal with systems that are too complex or too imprecise to be modeled using traditional binary logic. It is used in a wide range of applications, including control systems, decision-making systems, pattern recognition, and natural language processing.
How does Fuzzy Logic work?
Fuzzy logic works by assigning degrees of truth to statements or propositions. For example, in binary logic, the statement "the temperature is high" is either true or false. However, in fuzzy logic, the statement "the temperature is high" can be assigned a degree of truth based on how high the temperature is. If the temperature is very high, the degree of truth assigned to the statement would be close to 1.0 (or 100%), but if the temperature is only slightly high, the degree of truth would be lower.
Fuzzy logic uses membership functions to assign degrees of truth to statements. A membership function is a curve that represents the degree of membership of an element in a fuzzy set. For example, a membership function for the statement "the temperature is high" would be a curve that starts at 0 when the temperature is very low, increases to 1 when the temperature is very high, and levels off in between.
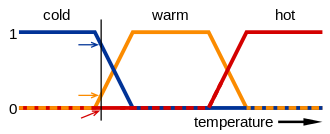
Fuzzy logic also uses operators to combine fuzzy propositions. The most common operators are AND, OR, and NOT. These operators are defined using fuzzy logic and are different from their binary logic counterparts.
Applications of Fuzzy Logic
Fuzzy logic is used in a wide range of applications, including:
- Control Systems: Fuzzy logic is used to control systems that are too complex to be modeled using traditional control theory. Examples include the control of temperature, humidity, and pressure in industrial processes.
- Decision-making Systems: Fuzzy logic is used in decision-making systems to make decisions based on incomplete or uncertain information. Examples include financial decision-making, medical diagnosis, and customer service.
- Pattern Recognition: Fuzzy logic is used in pattern recognition to classify objects or data based on fuzzy attributes. Examples include image recognition, speech recognition, and natural language processing.
Conclusion
Fuzzy logic is a powerful mathematical framework that allows for degrees of truth and uncertainty in decision-making and modeling complex systems. It has a wide range of applications, from control systems to natural language processing. While it can be complex, understanding the basics of fuzzy logic is essential for anyone interested in modeling or controlling complex systems.